Answer:
- Minimum and maximum temperatures are
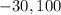
- Time taken to complete one complete cycle is 10 hours.
Explanation:
The general sinusoidal periodic function is,

here,
- amplitude = a,
- period =
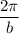 ,
, - horizontal or phase shift = c,
- vertical shift = d,
Comparing this with the given function
 , we get
, we get
- amplitude = a = 65,
- period =
 = 10,
= 10, - vertical shift = d = 35, so the axis of symmetry will be,
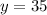
The maximum and minimum temperatures will be,
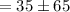
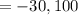
Time taken to complete one complete cycle is the period, so it is 10 hours.