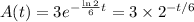If
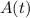
is the amount of oil in the well (let's say in millions of barrels) at time
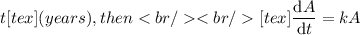
for some negative value of
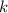
. You're told that the well started off with 3 million barrels, so

, and that after 6 years, there are 1.5 million barrels, so
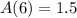
.
Solve the differential equation above:
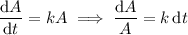
Integrate both sides.
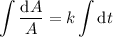
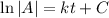

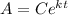
Given that

and
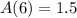
, you have
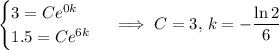
So the amount of oil in the well is given by the function