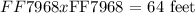We will determine how to evaluate the side length of a square given its area.
A square is a four sided 2D planar figure with all its sides at right angles and equal in magnitude as follows:
The side a square are all equal and will be denoted by a variable as follows:
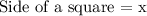
We will now express the Area of the square in terms of its side length using the basic definition as follows:
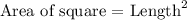
We will now express the above in terms of the side length variable ( x ) as follows:
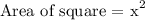
We are given that Natasha's garden has the following area:
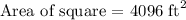
Now we will equate the result of area of a square with the side length ( x ) terms as follows:
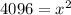
Evaluate(solve) the above the equation for the variable ( x ) by taking a square root on both sides of the equation as follows:
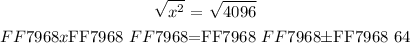
For practical sense, the variable ( x ) denotes the magnitude of the side length of the square which can not be negative. Hence, we have only solution for the side length ( x ) as follows: