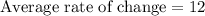Answer:
The correct order of the functions from least to greatest according to the average rate of change on the interval from x = -1 to x = 3 is:
g(x) , f(x) , h(x)
( Since,
average rate of change of g(x) is: 1/2
average rate of change of f(x) is: 8
average rate of change of h(x) is: 12 )
Explanation:
The average rate of a function from x=a to x=b is calculated by the formula:
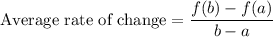
Here a= -1 and b=3
a)
The function f(x) is given by:
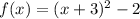
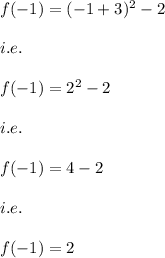

Hence, the average rate of change of f(x) is:
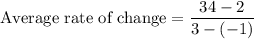
i.e.
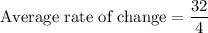
i.e.
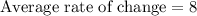
b)
The function g(x) is a straight line that passes through:
(-1,-2) and (3,0)
i.e.
g(-1)= -2
g(3)=0
i.e. the average rate of change is given by:
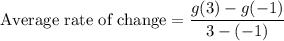
i.e.
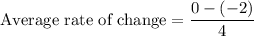
i.e.

i.e.
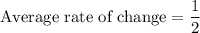
c)
Based on the table of values we have:
h(-1)= 14
and
h(3)= 62
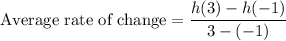
i.e.
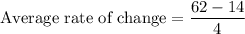
i.e.
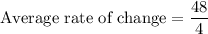
i.e.