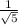Question

If tan Θ = 1 2 then what is sin Θ?

Answer 1

tanx=12 is the same as saying that tanx=12/1. We know that tanx is opposite over adjacent. If you draw out a triangle with x in an angle and 12 on the opposite length and 1 on the adjacent, pythagorean theorem can be used to find the hypotenuse, since sinx is opposite over hypotenuse. The hypotenuse is the square root of 145, and therefore sinx is 12/√145

Answer 2

Answer : The value of
`\sin \theta` is,
`(1)/(√(5))`

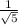
Step-by-step explanation :

Given:

`\tan \theta=(1)/(2)`

According to trigonometric function,

`\tan \theta=(Perpendicular)/(Base)=(1)/(2)`

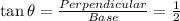
To make a ΔABC:

Thus,

Side AB = 1x

Side BC = 2x

Now we have to determine the side AC.

Using Pythagoras theorem in ΔABC :

`(Hypotenuse)^2=(Perpendicular)^2+(Base)^2`

`(AC)^2=(AB)^2+(BC)^2`

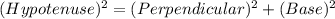
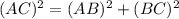
Now put all the values in the above expression, we get the value of side AC.

`(AC)^2=(1x)^2+(2x)^2`

`AC=√((1x)^2+(2x)^2)`

`AC=√(5)x`

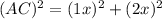
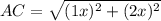
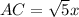
Now we have to determine the value of
`\sin \theta`

According to trigonometric function,

`\sin \theta=(Perpendicular)/(Hypotenuse)=(1x)/(√(5)x)`

`\sin \theta=(1)/(√(5))`

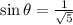
Thus, the value of
`\sin \theta` is,
`(1)/(√(5))`