Solution:
Given:
When the cardboard is folded to become a box (cuboid), it will have the following dimensions after the cut of squares from each corner;
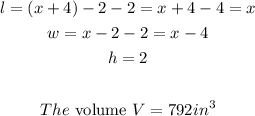
The volume of a cuboid is given by;

Solve the quadratic equation by factorization;

Hence, the dimension of the original piece of cardboard is;
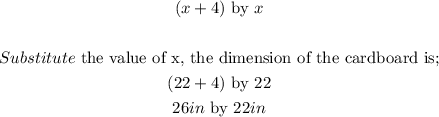
Therefore, the dimensions of the original piece of cardboard are 26 in by 22in