To find the slope of a line that passes through two points, we can use the following formula:
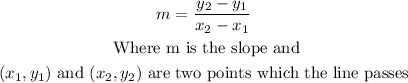
Then, we have:
First pair of lines
Line EF
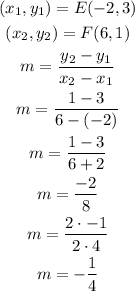
Line GH
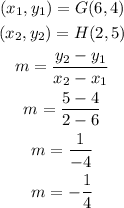
Now, when graphing the two lines, we have:
If two lines have equal slopes, then the lines are parallel. As we can see, their slopes are equal, therefore the lines EF and GH are parallel.
Second pair of lines
Line JK
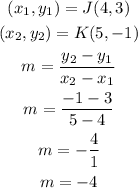
Line LM

Now, when graphing the two lines, we have:
As we can see, the slopes of these lines are different, so they are not parallel. Let us see if their respective slopes have the relationship shown below:
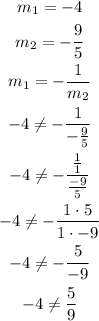
Since their respective slopes do not have the relationship shown below, then the lines are not perpendicular.
Third pair of lines
Line NP
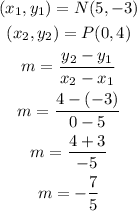
Line QR

Now, when graphing the two lines, we have:
Two lines are perpendicular if their slopes have the following relationship:
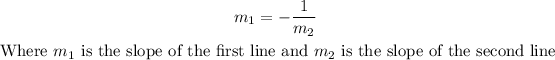
In this case, we have:
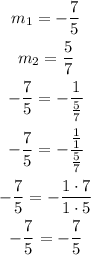
Since the slopes of the lines NP and QR satisfy the previous relationship, then this pair of lines are perpendicular.
Fourth pair of linesLine ST
![\begin{gathered} (x_1,y_1)=S\mleft(0,3\mright) \\ (x_2,y_2)=T\mleft(0,7\mright) \\ m=(y_2-y_1)/(x_2-x_1) \\ m=\frac{7-3_{}}{0-0} \\ m=(4)/(0) \\ \text{Undefined slope} \end{gathered}]()
The line ST has an indefinite slope because it is not possible to divide by zero. Lines that have an indefinite slope are vertical.
Line VW
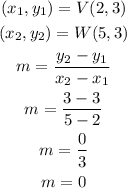
Line VW has a slope of 0. Lines that have a slope of 0 are horizontal.
Now, when graphing the two lines, we have:
As we can see in the graph, the ST and VW lines are perpendicular.