Question

What is the equation of the line that passes through the points (−2, 1) and (1, 10)?

Answer 1

Equation of the line will be y = 3x + 7

Explanation:

We have to find the equation of a line that passes through two points having coordinates as (-2, 1) and (1, 10) respectively.

Equation of the line in intercept form is represented by y = mx + c

Where m = slope of the line

c = y-intercept

Now we know slope of the line is represented by m =
`((y-y'))/((x-x'))`

m =
`((10-1))/((1+2))`

m =
`(9)/(3)`

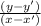
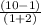
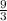
m = 3

Now the equation of the line will be y = 3x + c

Since point (1, 10) lies on the given line

So 10 = 3×1 + c

c = 10 - 3

c = 7

Finally the equation of the line will be y = 3x + 7