Question

Solve this system of ODEs by eliminating y.

Let D = y' , D² = y'', D³ = y''' etc.

D²x - Dy =
`e^(2t)` - 6t

Dx + Dy = y - x + 3
`e^(2t)`

Answer 1

`\begin{cases}{\mathrm D}^2x-{\mathrm D}y=e^(2t)-6t\\{\mathrm D}x+{\mathrm D}y=y-x+3e^(2t)\end{cases}`

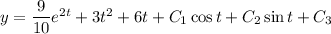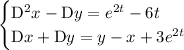
Adding the two ODEs gives


`{\mathrm D}^2x+{\mathrm D}x=y-x+4e^(2t)-6t`

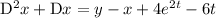
Differentiating once gives


`{\mathrm D}^3x+{\mathrm D}^2x={\mathrm D}y-{\mathrm D}x+8e^(2t)-6`

`{\mathrm D}^3x+{\mathrm D}^2x-{\mathrm D}y+{\mathrm D}x=8e^(2t)-6`

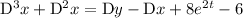
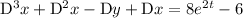
The first ODE lets you simplify this a bit:


`{\mathrm D}^3x+e^(2t)-6t+{\mathrm D}x=8e^(2t)-6`

`{\mathrm D}^3x+{\mathrm D}x=7e^(2t)+6t-6`

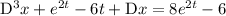
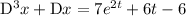
Let
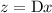
`z={\mathrm D}x`, so that
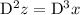
`{\mathrm D}^2z={\mathrm D}^3x`, and reduce the order of the ODE to get


`{\mathrm D}^2z+z=7e^(2t)+6t-6`

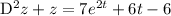
Solving this ODE for
`z` shouldn't be a problem for you; you would find that


`z=C_1\cos t+C_2\sin t+\frac75e^(2t)+6t-6`

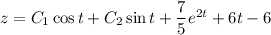
Since
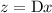
`z={\mathrm D}x`, integrating once with respect to
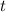
`t` gives the general solution for
`x`:


`x=C_1\sin t-C_2\cos t+\frac7{10}e^(2t)+3t^2-6t+C_3`

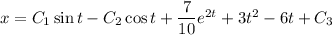
Now plug in the second derivative of this solution into the first ODE to find another ODE in
`y` alone.


`{\mathrm D}^2x=-C_1\sin t+C_2\cos t+\frac{14}5e^(2t)+6`


`-C_1\sin t+C_2\cos t+\frac{14}5e^(2t)+6-{\mathrm D}y=e^(2t)-6t`

`{\mathrm D}y=\frac95e^(2t)+6t+6-C_1\sin t+C_2\cos t`

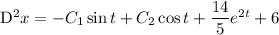
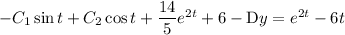
Integrate with respect to
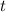
`t` and you get


`y=\frac9{10}e^(2t)+3t^2+6t+C_1\cos t+C_2\sin t+C_3`