Question

David has available 520 yards of fencing and wishes to enclose a rectangular area(a) Express the area A of the rectangle as a function of the width W of the rectangle(b) For what value of W is the area largest?(c) What is the maximum area?

Answer 1

The perimeter of a rectangle is calculated by adding all the lengths of its sides.

`P=2l+2w`

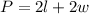
So, if David has 520 yards available of fencing to enclose the perimeter of a rectangular area, we can say that:

`520yd=2l+2w`

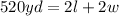
Simplifying the equation above, we can rewrite it into:

`\begin{gathered} 520yd=2(l+w) \\ \text{Divide both sides by 2.} \\ 260=l+w \end{gathered}`

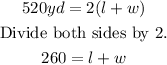
This will be our equation 1: 260 = l + w.

On the other hand, to get the area of the rectangle, the formula is:

`\begin{gathered} A=\text{length}* width \\ A=l* w \end{gathered}`

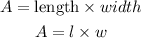
Now, based on equation 1, we can derive the value of the length into:

`\begin{gathered} 260=l+w \\ l=260-w \end{gathered}`

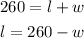
Having this value of the length, we can plug this into the formula of the area.

`\begin{gathered} A=l* w \\ \text{Plug in the value of l.} \\ A=(260-w)* w \\ \text{Simplify.} \\ A=260w-w^2 \\ \text{Rearrange.} \\ A=-w^2+260w \end{gathered}`

a. A = -w² + 260w is the equation that expresses the area of the rectangle as a function of the width W.

The quadratic equation above is in its general form:

`ax^2+bx+c=0`

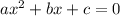
in which a = -1, b = 260, and c = 0 since there is no constant term.

Since the value of "a" is negative, this means that the graph of this equation which is parabola is opening downward. To determine what value of "w" will give us the maximum area "A", we have to locate the x-coordinate of the vertex of this parabola. The formula is:

`x=-(b)/(2a)`

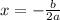
Since we have already identified the value of "a" and "b" in our equation, let's plug them into the formula above.

`x=-(260)/(2(-1))=-(260)/(-2)=130`

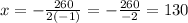
Hence, the x-coordinate of the vertex is 130. This will be the value of w.

b. At w = 130 yards, the area is the largest.

c. To calculate the area, simply plug w = 130 into our quadratic equation above.

`\begin{gathered} A=-w^2+260w \\ A=-(130)^2+260(130) \\ A=-16900+33800 \\ A=16,900 \end{gathered}`

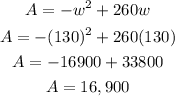
The maximum area of the rectangle is 16,900 square yards.