Question

Solve the inequality and graph the solution set on a real number line. Express the solution set in interval notation.x2 + 3x - 297 > 25The solution set is(Type your answer in interval notation. Use integers or fractions for any numbers in the expression.)

Answer 1

In order to solve this inequality, we have to use the definition of the absolute value function, that is:

|f(x)| > a ⇒ f(x) > a , f(x) < -a

Applying this to our expression, we get:

`\begin{gathered} \lvert x^2+3x-29\rvert>25 \\ x^2+3x-29>25,x^2+3x-29<-25 \end{gathered}`

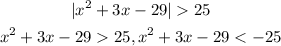
We got two inequalities:

1) x^2 + 3x - 29 > 25

2) x^2 + 3x - 29 < -25

Let's solve the first one, first, we have to rewrite the equation so there is a 0 on the right side:

x^2 + 3x - 29 > 25

x^2 + 3x - 29 - 25 > 25 - 25

x^2 + 3x - 54 > 0

In order to solve this, we can apply the quadratic equation, like this:

`\begin{gathered} \frac{-b\pm\sqrt[]{b^2-4ac}}{2c} \\ \frac{-3\pm\sqrt[]{(3)^2-4*1*(-54)}}{2*1}=(-3\pm15)/(2) \\ x1=(-3+15)/(2)=(12)/(2)=6 \\ x2=(-3-15)/(2)=(-18)/(2)=-9 \end{gathered}`

Since a>0 (1, the number that multiplies x^2) then the parabola opens upwards, then the above inequality is true if x<-9 or x>6.

Now, let's solve the second inequality, similarly as for the previous one, we get:

x^2 + 3x - 29 < -25

x^2 + 3x - 4 < 0

Applying the quadratic formula, we get the solutions of this inequality, x1 = 1 and x2= -4.

Then, the inequality is true if x<1 and x>-4 (-4

Mixing the two domains:

-46)

x<-9 or -46

As you can see, the domain has 3 different areas, from -∞ to -9 (-∞, -9), from -4 to 1 (-4, 1) and from 6 to ∞ (6, ∞), then the solution set in interval notation is:

(-∞, -9), (-4, 1), (6, ∞).

We can graph this solution set on a real number line, like this: