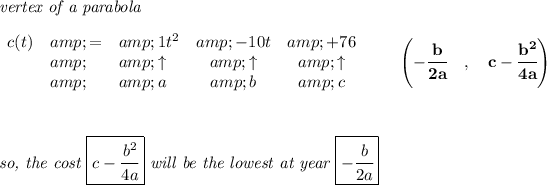Question

Emily invested in Google Stock (in the thousands of dollars) between the years 2000- 2013. The value of the stock can be modeled by the equation c(t)=t^2 -10t+76, where t=0 represents 2000. In what year did the stock reach its minimum value? What is the minimum value?

Answer 1

the c(t) equation, as you can see, is a quadratic equation, and thus its graph is a parabola, the leading term's coefficient is positive, so the parabola looks like the picture below

and the lowest point is at the vertex
c(t) reaches it's lowest point there


`\bf \textit{vertex of a parabola}\\ \quad \\ \begin{array}{lllccllll} c(t)&=&1t^2&-10t&+76\\ &&\uparrow &\uparrow &\uparrow \\ &&a&b&c \end{array} \qquad \left(-\cfrac{{{ b}}}{2{{ a}}}\quad ,\quad {{ c}}-\cfrac{{{ b}}^2}{4{{ a}}}\right) \\\\\\\\ \textit{so, the cost } \boxed{{{ c}}-\cfrac{{{ b}}^2}{4{{ a}}}}\textit{ will be the lowest at year }\boxed{-\cfrac{{{ b}}}{2{{ a}}}}`