Question

Which of the following shows the equation 6^2=35 in logarithmic form

Answer 1

I converted it and it a log^6(35)=2

Answer 2

The logarithmic form of the equation
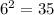`\(6^2 = 35\)` is
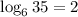`\(\log_6 35 = 2\)`, indicating that the logarithm of 35 with base 6 equals 2, providing a concise representation of the exponentiation relationship.

The equation
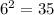`\(6^2 = 35\)` can be expressed in logarithmic form using the base 6 logarithm. The logarithmic form of
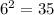`\(6^2 = 35\)` is written as
`\(\log_6 35 = 2\)`.

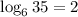In general, if
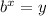`\(b^x = y\)`, then the logarithmic form is
`\(\log_b y = x\)`. In this specific case,
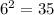`\(6^2 = 35\)` can be translated to
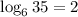`\(\log_6 35 = 2\)`, which is saying that the logarithm with base 6 of 35 is equal to 2.

This means that 6 raised to the power of 2 equals 35, and conversely, the logarithm of 35 to the base 6 is 2. The logarithmic form provides a way to represent exponentiation in a concise and mathematical way, helping in various mathematical and computational applications.

The probable question may be:

Write the equation 6^2=35 in logarithmic form.