Question

Find the value of n that makes each equation true. Then, arrange the equations in increasing order of the values of n found. Tiles 2n = 35n = 20n + 5 = 13n + 5 = 10

Answer 1

solve for substitution

2n = 35n = 20n + 5 = 13n + 5 = 10

or

solve for n

n = 5

Answer 2

n = 5 > n = 0.384 > n = 0.285 > n = 0.25

Explanation:

We are given the equation,

`2n = 35n = 20n + 5 = 13n + 5 = 10`

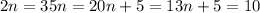
Solving, each equation for n,

`2n = 10\\n = (10)/(2) \\n = 5`

`35n = 10\\n = (10)/(35) \\\\n = (2)/(7)\\\\n = 0.285`

`20n + 5 =10\\20n = 10-5\\ n = (5)/(20)\\\\n = 0.25`

`13n + 5 = 10\\13n = 5\\n = (5)/(13) \\n = 0.384\\`

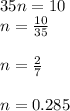
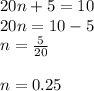
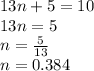
We have found different solutions of n for different equations.

Now, ultimately all these equations are equated to 10, thus all have the same value of 10, thus it cannot be arranged in increasing order as they all equations equal value of 10.