Question

3) 46.7 L of a gas is initially at a pressure of 662 torr and a temperature of 266 K. If the volume decreases to 35.0 L and the temperature increases to 342 K, what is the new pressure?​

Answer 1

The new pressure is 1,135.67 torr

Step-by-step explanation:

Boyle's law establishes the relationship between pressure and volume of a gas when the temperature is constant, establishing that the pressure of a gas in a closed container is inversely proportional to the volume of the container. Mathematically, this law says that the product of pressure and volume is constant:

P*V=k

Charles's law establishes the relationship between the temperature and the volume of a gas when the pressure is constant. This law states that the volume is directly proportional to the temperature of the gas. So, Charles's law says that the quotient that exists between the volume and the temperature will always have the same value:

`(V)/(T) =k`

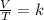
Finally, Gay-Lussac's Law is a gas law that relates pressure and temperature at constant volume. This law says that the pressure of the gas is directly proportional to its temperature:

`(P)/(T) =k`

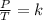
Combined law equation is the combination of three gas laws called Boyle's, Charlie's and Gay-Lusac's law:

`(P*V)/(T) =k`

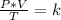
Analyzing an initial state 1 and a final state 2, it is satisfied:

`(P1*V1)/(T1) =(P2*V2)/(T2)`

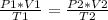
In this case:

• P1= 662 torr
• V1= 46.7 L
• T1= 266 K
• P2= ?
• V2= 35 L
• T2= 342 K

Replacing:

`(662 torr*46.7 L)/(266 K) =(P2*35 L)/(342 K)`

Solving:

`P2=(342 K)/(35 L) *(662 torr*46.7 L)/(266 K)`

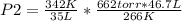
P2= 1,135.67 torr

The new pressure is 1,135.67 torr