Answer:
The correct options are A, B and E.
Explanation:
The given function is
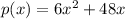
Vertex form of the function is
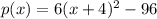 ..... (1)
..... (1)
The vertex form of a parabola is
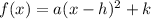 ..... (2)
..... (2)
where, (h,k) is vertex and x=h is the axis of symmetry.
If a>0, then parabola opens up and if a<0, then parabola opens down.
If |a|>1, then graph is narrower than the graph of
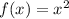 and if |a|<1, then graph is wider than the graph
and if |a|<1, then graph is wider than the graph
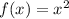 .
.
From (1) and (2), it is clear that
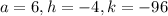
So we conclude that
1. The axis of symmetry is the line x = –4.
2. The graph is narrower than the graph of
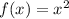 .
.
3. The parabola has a minimum.
4. The parabola opens up.
5. The value of k is –96, so there is a vertical shift down 96 units.
Therefore options A, B and E are correct.