Question

Instructions:Select the correct answer from each drop-down menu. Please help

Answer 1

1. the invalid relation is the 4th choice

2. you can conclude that the 2nd choice is correct.

Answer 2

Option 4

Option 2

Explanation:

Given: The line segment AB and CD, P is the midpoint of AB which implies AP=PB and Q is the midpoint of CD which implies CQ=QD.

Also, It is given that P is point on AB, therefore there is no relation of point P with line segment CQ.

Hence, the invalid statement is

Segment AP is congruent to segment PQ.

Therefore, option (D) is correct.

Now, it is given that R is the midpoint of AP which implies AR=RP and S is the midpoint of QD which implies QS=SD

Now, AB≅CD (Given)

`(1)/(2)AB`≅
`(1)/(2)CD`

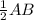PB≅CQ (Mid points are given)

Therefore, PA=QD

⇒PR=QS

Also, because PB≅CQ⇒PB+PR≅CQ+QS

⇒RB≅CS

⇒Segment RB is congruent to segment CS

Hence, option 2 is correct.