Question

What is the 7th term of the geometric sequence where a1 = 1,024 and a4 = −16?

Answer 1

-16=ar^4 divided by 1024=ar is:

-1/64=r^3

r=-1/4

1024=a(-1/4), a=-4096 so

a(n)=-4096(-0.25^n)

a(7)=-4096(-0.25^7)=0.25

Answer 2

the 7th term of the geometric sequence is 1/4 or 0.25

Explanation:

Given geometric sequence terms

a1 = 1,024 and a4 = −16

nth term of geometric sequence is

`a_n= a_1(r)^(n-1)`

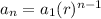
a1 = 1,024 and a4 = −16

Plug in 4 for n and solve for 'r'

`a_4= a_1(r)^(4-1)`

`-16= 1024(r)^(3)`

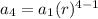
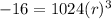
Divide both sides by 1024

`(-1)/(64) = r^3`

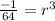
Now take cube root on both sides

`(-1)/(4) = r`

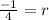
To find 7th term we plug in n=7 , r= -1/4 , a1 = 1024

`a_n= a_1(r)^(n-1)`

`a_7= 1024(-1/4)^(7-1)`

`a_7= 1024(-1/4)^(6)`

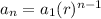
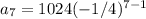
a_7 = 0.25