Question

How many positive integers $n$ satisfy $127 \equiv 7 \pmod{n}$? $n=1$ is allowed.

Answer 1

`127\equiv7\mod n` means there is some positive integer
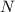
`N` such that
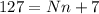
`127=Nn+7`. Equivalently, there's some
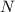
`N` such that
`Nn=120`.

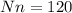
This would mean any such number that satisfies the modular congruence must be a positive divisor of 120. There 16 of them:


`\{1,2,3,4,5,6,8,10,12,15,20,24,30,40,60,120\}`

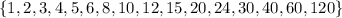
But the congruence doesn't hold for all of these simply because
`127\equiv7\mod n` can't be true for any
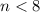
`n<8`. This shrinks the pool of candidates to the set


`\{8,10,12,15,20,24,30,40,60,120\}`

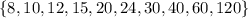
so there are 10 possible solutions for
`n`.