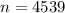We are given
Proportion (p)
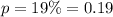
Level of significance = 99%
margin of error = 1.5% = 0.015
We want to find n
Solution
Note: The margin of error formula is given as
![MarginOfError=z_{(\alpha)/(2)}*\sqrt[]{(p(1-p))/(n)}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/vrzax6rip7l9bdf7669i.png)
The image of the formula to use is
In the question, we have


Substituting the parameters
![\begin{gathered} MarginOfError=z_{(\alpha)/(2)}*\sqrt[]{(p(1-p))/(n)} \\ 0.015=2.576*\sqrt[]{(0.19(1-0.19))/(n)} \\ \sqrt[]{(0.19(1-0.19))/(n)}=(0.015)/(2.576) \\ (0.19(0.81))/(n)=((15)/(2576))^2 \\ (n)/(0.19(0.81))=((2576)/(15))^2 \\ n=0.19(0.81)((2576)/(15))^2 \\ n=4538.870784 \\ n=4539\text{ (to the nearest whole number)} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/5j6wt1rxhhbceer1spsw.png)
Therefore, the sample size is as large as