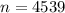Question

You want to obtain a sample to estimate a population proportion. Based on previous evidence, you believethe population proportion is approximately 19%. You would like to be 99% confident that your estimate is within 1.5% of the true population proportion. How large of a sample size is required? Do not round mid-calculation.n

Answer 1

We are given

Proportion (p)

`p=19\%=0.19`

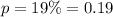
Level of significance = 99%

margin of error = 1.5% = 0.015

We want to find n

Solution

Note: The margin of error formula is given as

`MarginOfError=z_{(\alpha)/(2)}*\sqrt[]{(p(1-p))/(n)}`

The image of the formula to use is

In the question, we have

`\begin{gathered} \alpha=0.01 \\ \text{from the statistics table} \\ z_{(\alpha)/(2)}=z_{(0.01)/(2)}=z_(0.005)=2.576 \end{gathered}`
`\begin{gathered} p=0.19 \\ MarginOfError=0.015 \end{gathered}`

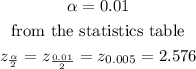
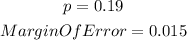
Substituting the parameters

`\begin{gathered} MarginOfError=z_{(\alpha)/(2)}*\sqrt[]{(p(1-p))/(n)} \\ 0.015=2.576*\sqrt[]{(0.19(1-0.19))/(n)} \\ \sqrt[]{(0.19(1-0.19))/(n)}=(0.015)/(2.576) \\ (0.19(0.81))/(n)=((15)/(2576))^2 \\ (n)/(0.19(0.81))=((2576)/(15))^2 \\ n=0.19(0.81)((2576)/(15))^2 \\ n=4538.870784 \\ n=4539\text{ (to the nearest whole number)} \end{gathered}`

Therefore, the sample size is as large as

`n=4539`