Question

Line A passes through points(1 , 10) and (6, 3). Line B is perpendicular to A. what is the slope of line B?

Answer 1

Answer:

The slope of line B = 5/7

Explanations:

Line A passes through the points (1, 10) and (6, 3)

The slope of a line passing though the points (x₁, y₁) and (x₂, y₂) is given by the formula:

`m\text{ = }(y_2-y_1)/(x_2-x_1)`
`\begin{gathered} \text{Let the slope of the line A passing thorugh the points (1,10) and (6,3) be m}_A \\ _{} \end{gathered}`

`\begin{gathered} m_A=\text{ }(3-10)/(6-1) \\ m_A=\text{ }(-7)/(5) \end{gathered}`

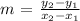
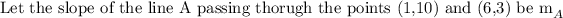
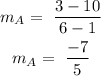
When two lines are perpendicular, the slope of one is the negative inverse of the other.

Since line B is perpendicular to line A:

`\begin{gathered} m_B=\text{ }(-1)/(m_A) \\ m_B=\text{ -1 }/\text{ }(-7)/(5) \\ m_B=\text{ -1 }*(-5)/(7) \\ m_B=\text{ }(5)/(7) \end{gathered}`

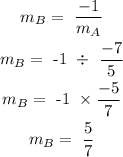
The slope of line B = 5/7