Question

A sphere and a right cylinder have the same radius and volume. The cylinder has a height of 3 inches. Find the radius.

Answer 1

V sphere = 4/3 pi r^3

V cyl = pi r^2 * h

4/3 pi r^3 = pi r^2 * h
4/3 r =h

h=3

so: r = 3 *3 / 4 = 2.25 in

Answer 2

The radius of the sphere and cylinder is 2.25 inches.

Explanation:

It is given that sphere and a right cylinder have the same radius and volume.

Let the radius of the sphere and cylinder be r.

The volume of the sphere is

`V_1=(4)/(3)\pi r^3`

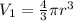
The volume of the cylinder is

`V_2=\pi r^2h`

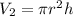
The cylinder has a height of 3 inches.

`V_2=\pi r^2(3)=3\pi r^2`

`V_1=V_2`

`(4)/(3)\pi r^3=3\pi r^2`

`4\pi r^3=9\pi r^2`

`(\pi r^3)/(\pi r^2)=(9)/(4)`

`r=(9)/(4)=2.25`

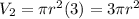
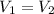
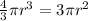
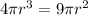
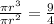
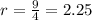
Therefore radius of the sphere and cylinder is 2.25 inches.