Question

What is the range of y = –3sin(x) – 4?

Answer 1

What is the range of y = –3sin(x) – 4?

[-7,-1]
y

Answer 2

Answer: [-7,-1]

Explanation:

range of a function is that limit in which variation of any function is possible.

general range of sinx is between [-1,1]

-1
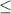`\leq`sinx
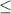`\leq`1 (A)

our required function is y= -3sinx - 4

So, as to obtain this function we will multiply the each side in Equation (A) by -3 we will get

-3
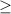`\geq`-3sinx
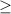`\geq`3 (B)

now subtract from 4 from each side of (B) we will get

-7
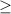`\geq`-3sinx-4
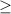`\geq`-1

Hence, required range of the given function y= -3sinx-4 is [-7,-1].