Question

HELP

The table gives the distance between a lighthouse and a cruise ship at different times. The cruise ship is traveling at a uniform speed.

Complete the following sentences based on the data in the table.

Distance from Lighthouse
(nautical miles)
2 53
4 95.5
6 138
10 223
12 265.5

After 11 hours, the cruise ship will be ____ nautical miles from the lighthouse.

At the start of the journey, the cruise ship was ____ nautical miles from the lighthouse.

The cruise ship is traveling at a speed of ___ nautical miles per hour.

Answer 1

I believe the answer is the ship is traveling at 21.25 MPH, started 10.5 miles from lighthouse and after 11 hours will be 244.25 miles from the lighthouse.

Answer 2

Ques 1)

After 11 hours, the cruise ship will be 244.25 nautical miles from the lighthouse.

Ques 2)

At the start of the journey, the cruise ship was 10.5 nautical miles from the lighthouse.

Ques 3)

The cruise ship is traveling at a speed of 21.25 nautical miles per hour.

Explanation:

We are given a table that represents the number of hours and distance from the Lighthouse as:

Time (in hours) Distance from Lighthouse

(nautical miles)

2 53

4 95.5

6 138

10 223

12 265.5

As the speed is uniform hence, we can find the equation that represents the distance in term of the number of hours.

( As the speed is uniform hence, we get a constant slope i.e. we get a equation of a line)

As we know that the equation of a line passing through two points (a,b) and (c,d) is given by:

`y-b=(d-b)/(b-a)* (x-a)`

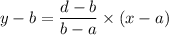
Let (a,b)=(2,53) and (c,d)=(4,95.5)

where y denote the distance from lighthouse and x denotes the number of hours.

Hence, the equation of line is:

`y-53=(95.5-53)/(4-2)* (x-2)\\\\\\y-53=21.25(x-2)\\\\y-53=21.25x-42.5\\\\y=21.25-42.5+53\\\\y=21.25x+10.5`

• Now when x=11 we have:

`y=21.25* 11+10.5\\\\\\y=244.25`

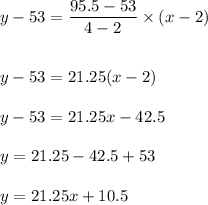
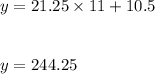
Hence,

After 11 hours, the cruise ship will be 244.25 nautical miles from the lighthouse.

• Now when x=0 we have:

`y=21.25* 0+10.5\\\\\\y=10.5`

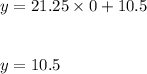
Hence,

At the start of the journey, the cruise ship was 10.5 nautical miles from the lighthouse.

• Now the speed of the cruise ship is equal to the slope of the equation.

We have slope=21.25

Hence,

The cruise ship is traveling at a speed of 21.25 nautical miles per hour.