Question

Which of the following expressions represents the LCM of 91x 2 y and 104xy 3? 13xy 728x 2y 3 13x 2y 728xy

Answer 1

728x^2y^3 is your answer

Answer 2

Answer: the correct option is (B)
`728x^2y^3.`

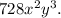
Step-by-step explanation: We are given to select the correct L.C.M. of the following expressions :

`91x^2y~~~~~~\textup{and}~~~~~104xy^3.`

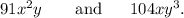
We know that

L.C.M. stands for the least common multiple.

Now, the prime factorization of the given expressions are as follows :

`91x^2y=7*13* x * x * y,\\\\104xy^3=2* 2*2* 13* x * y* y* y.`

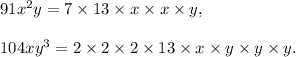
Therefore, the required L.C.M will be

`L.C.M.=2*2*2*7*13* x* x* y* y* y=728x^2y^3.`

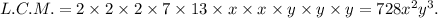
Thus, the L.C.M. of he given expressions is
`728x^2y^3.`

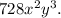
Option (B) is CORRECT.