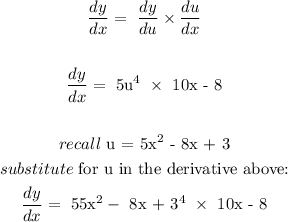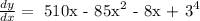Question

Yea I can do tomorrow it would be nice

Answer 1

Answer:
`(dy)/(dx)=\text{ 5\lparen10x - 8\rparen\lparen5x}^2\text{ - 8x + 3\rparen}^4`

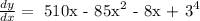
See other answers for the blanks below

Step-by-step explanation:

Given:

`y\text{ = \lparen5x}^2-\text{ 8x + 3\rparen}^5`

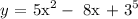
To find:

derivative of the function = dy/dx

To determine the derivative, we will follow the steps provided in the question

`\begin{gathered} a)\text{ }let\text{ the inside = expression in the parenthesis} \\ \text{inside: u = 5x}^2\text{ - 8x + 3} \\ \\ Substitute\text{ for u} \\ y\text{ = u}^5 \\ outside:\text{ y = u}^5 \end{gathered}`

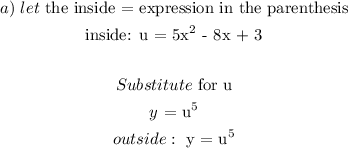
b) Next is to find the derivative of the outside and insides:

`\begin{gathered} inside:\text{ u = 5x}^2\text{ - 8x + 3} \\ (du)/(dx)\text{ = 10x - 8} \\ \\ outside:\text{ y = u}^5 \\ (dy)/(du)\text{ = 5u}^(5-1) \\ (dy)/(du)\text{ = 5u}^4 \end{gathered}`

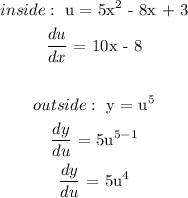
c) We will use the chain rule formula to get the derivative:

`\begin{gathered} (dy)/(dx)=\text{ }(dy)/(du)*(du)/(dx) \\ \\ (dy)/(dx)=\text{ 5u}^4\text{ }*\text{ \lparen10x - 8\rparen} \\ \\ recall\text{ u = 5x}^2\text{ - 8x + 3} \\ substitute\text{ for u in the derivative above:} \\ (dy)/(dx)=\text{ 5\lparen5x}^2-\text{ 8x + 3\rparen}^4\text{ }*\text{ \lparen10x - 8\rparen} \end{gathered}`
`(dy)/(dx)=\text{ 5\lparen10x - 8\rparen\lparen5x}^2\text{ - 8x + 3\rparen}^4`