Question

Which of the following expressions represents the GCF of 91x 2 y and 104xy 3?

13xy
728x 2y 3
13x 2y
728xy

Answer 1

The greatest common factor is found by finding the product of common primes.

91=7*13, 104=2*2*2*13 so the gcf of 91 and 104 is 13. Since the highest power of x and y in both terms is 1, the hcf for the variables is just xy

13xy

Answer 2

Answer: The correct option is (A) 13xy.

Step-by-step explanation: We are given to select the greatest common factor (G.C.F) of the following two expressions :

`91x^2y~~~~\textup{and}~~~~104xy^3.`

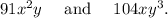
The G.C.F. of two numbers is the product of the common terms in the prime factorization of the expressions.

We have

`91x^2y=7* 13* x* x* y,\\\\104xy^3=2*2*2*13* x* y* y* y.`

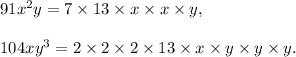
Therefore, the G.C.F. of the given expressions will be

`G.C.F.=13* x* y=13xy.`

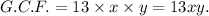
Thus, the required G.C.F is 13xy.

Option (A) is CORRECT.