Question

Write a system of equations to describe the situation below, solve using any method, and fill in the blanks.An online boutique is having a special on personalized baby items. On Monday, they sold 24 personalized baby blankets and 2 personalized hooded towels, for a total of $790 in receipts. The following day, they received orders for 24 personalized baby blankets and 4 personalized hooded towels, which brought in a total of $836. How much does each item sell for?

Answer 1

The Solution:

Let the cost of each baby blanket be x and that of each hooded towel be y.

Given:

24 personalized baby blankets and 2 personalized hooded towels sold for a total cost of $790. We have the equation as below:

`24x+2y=790\ldots\text{eqn}(1)`

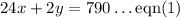
24 personalized baby blankets and 4 personalized hooded towels sold for a total cost of $836. We have the equation as below:

`24x+4y=836\ldots\text{eqn}(2)`

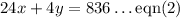
So, the system of equations that describe the situation is:

`\begin{gathered} 24x+2y=790 \\ 24x+4y=836 \end{gathered}`

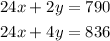
To find the cost of each of the items, we shall solve the pair of equations simultaneously.

By the Elimination Method of solving simultaneous equations, we shall subtract eqn(1) from eqn(2). That is,

`\begin{gathered} 24x+4y=836 \\ -(24x+2y=790) \\ ----------- \\ 2y=46 \end{gathered}`

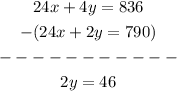
Dividing both sides by 2, we get

`\begin{gathered} y=(46)/(2)=23 \\ \text{ So, each personalized hooded towel sells for \$23} \end{gathered}`

To find the value of x, we shall substitute 23 for y in eqn(1).

`\begin{gathered} 24x+2(23)=790 \\ 24x+46=790 \end{gathered}`

Subtracting 46 from both sides, we get

`\begin{gathered} 24x+46-46=790-46 \\ 24x=744 \end{gathered}`

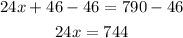
Dividing both sides by 24, we get

`\begin{gathered} x=(744)/(24)=31=\text{ \$31} \\ \text{ So, each personalized baby blanket sells for \$31} \end{gathered}`

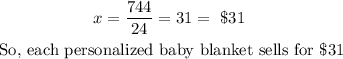
Therefore, the correct answer are:

Each personalized baby blanket sells for $31

Each personalized hooded towel sells for $23