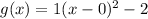Question

Find g(x), where g(x) is the translation 2 units left of f(x)=x2.Write your answer in the form a(x–h)2+k, where a, h, and k are integers.

Answer 1

Write your answer in the form a(x–h)2+k, where a, h, and k are integers.

Explanation:

Given:

The function

`f(x)=x^2`

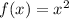
A standard parabola with vertex at origin is represented as:

`f(x)=ax^2`

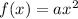
The above function is a standard parabola with vertex at origin and opening upward.

The vertex of the above function is at the origin ( 0 , 0) and the value of is 1.

Now, the function is translated 2 units left

So, from the rule of function transformations, if a graph is moved up by units, then units is added to the function.

Therefore,

`\begin{gathered} g(x)=f(x)-2 \\ g(x)=x^2-2 \end{gathered}`

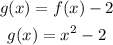
Also, the vertex of f(x) will be translated 2 units left. So, the co-ordinates of the vertex of g(x) will be (0 , 0-2) = (0,-2)

Now, express the above function in the vertex form

`g(x)=a(x-h)^2+k`

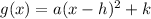
now we have a = 1, h = 0, k = -2

This gives

`g(x)=1(x-0)^2-2`