Question

Wendy has 180 feet of fencing. She needs to enclose a rectangular space with an area that is ten times its perimeter. If she uses up all her fencing material, how many feet is the largest side of the enclosure?

Answer 1

Okay well we know she will use all of her fencing, so the total will be 180 like so.
180 = p.
(since it will only cover the perimeter of the rectangular area)

and let's call perimeter p and area a.
we know that A = 10p.
Also, we know P = a/10.
Since 180 = p, and p = a/10, we can set them equal to each other to solve for a.

180 = a/10
1800 = a. The area is 1,800 square feet.

(Remember, we know the perimeter is 180 feet).

Work from earlier:
P=2(b + h)=180A=bh=10∗P=10∗180=1800 b+h=90b∗h=1800

So the area is 1800 and the perimeter is 90.
So, we know that 90 = 2(40 + 5)
So the longer side will be 40 feet.

Answer 2

60 feet is the largest side of the enclosure.

Explanation:

Length of rectangle space = l

Breadth of rectangular space = b

Area of the rectangle = A

A = lb

Perimeter of the rectangular space ,P = 180 ft

Perimeter of the rectangle = 2(l+b)

`A=10* p=10* 180 ft=1800 ft^2`

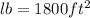`lb = 1800 ft^2`...[1]

2(l+b)=180 ft

l + b = 90 ft...[2]

On putting value of b from [1] into [2] , we get:

`l+(1800)/(l)=90`

`l^2+1800=90l`

`l^2-90l+1800=0`

`l^2-60l-30l+1800=0`

`l(l-60)-30(l-60)=0`

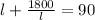
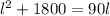
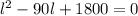
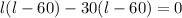
(l-30)(l-60)=0

l = 60 ft, 30 ft

Length is the longest side of the rectangle. So length of the rectangle is 60 feet.