Question

In centimeters, what is the unknown length in this right triangle?

HELP ASAP ,THERE IS NO A,B,C,D ANSWER ITS A WRITTEN RESPONSE OF THE NUMBER

Answer 1

The work out the length of the missing side you need to use Pythagoras' theorem which states that the sum of the squares of the two sides, in this case x and 60, is equal to the sum of the square of the hypotenuse. This can be formulated as
`a^(2) +b^(2)=c^(2)`. In this case x can replace a or b (I've replaced a).

`x^(2) +b^(2)=c^(2)`
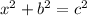
To solve for x rearrange the equation by subtracting
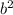
`b^(2)` from both sides:

`c^(2) -b^(2)=x^(2)`
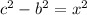
Substitute the numbers in:

`x^(2) = 61^(2) -60^(2)`
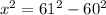
= 3721-3600
= 121
Take the square root of 121 to find x:
x =
`√(121)`
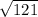
= 11cm

Answer 2

11

Step-by-step explanation:

Using the Pythagorean Theorem,

a² + b² = c² is the same as c² - b² = a²

c = 61

61^2 = 61 X 61 = 3,721

b = 60

60^2 = 60 X 60 = 3,600

Next, we subtract:

3,721 - 3,600 = 121

√121 = 11

(x = 11 cm)

so 11 is your answer