According to the Law of Conservation of Energy, the total energy input must be equal to the total energy output. The energy input is equal to the 380J extracted from the hot reservoir. The energy output includes the energy delivered to the cold reservoir and the work done. Then:
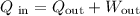
Substitute Q_in=380J and Q_out=120J to find the amount of energy converted to work:
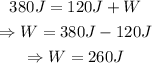
Remember that for a reversible heat engine:
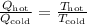
In this case, we know that Q_hot=380J, Q_cold=120J and T_cold=850K. Isolate T_hot from the equation and substitute the values of each variable to find the temperature of the hot reservoir:
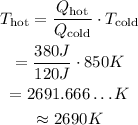
Therefore, 260 Joules are converted to work and the temperature of the hot reservoir is 2690K.