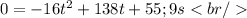Question

A rocket is launched from the top of a 55-foot cliff with an initial velocity of 138 ft/s.

a. Substitute the values into the vertical motion formula h = –16t2 + vt + c. Let h = 0.
b. Use the quadratic formula to find out how long the rocket will take to hit the ground after it is launched. Round to the nearest tenth of a second.

Answer Choices:
A. 0 = –16t2 + 55t + 138; 0.4 s
B. 0 = –16t2 + 55t + 138; 9 s
C. 0 = –16t2 + 138t + 55; 0.4 s
D. 0 = –16t2 + 138t + 55; 9 s

Answer 1

Answer:D. 0 = –16t2 + 138t + 55; 9 s

Answer 2

For this case we have that the equation that describes the height is:

`image`

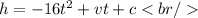
Where,

v: initial speed

c: initial height

Substituting values we have:

`image`

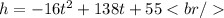
Then, to find the time, we use the quadratic formula:

`t =(-b +/-√(b^2 - 4ac) )/(2a)`

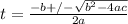
Substituting values we have:

`t =(-138 +/-√(138^2 - 4(-16)(55)) )/(2(-16))`

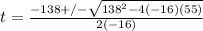
Rewriting:

`t =(-138 +/-√(19044 + 3520) )/(-32)`

`t =(-138 +/-√(22564))/(-32)`

`t =(-138 +/-150.21)/(-32)`

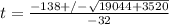
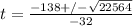
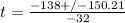
We discard the negative root because we want to find the time.

We have then:

`t =(-138 -150.21)/(-32)`

`image`

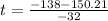
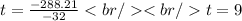
Answer:

D.
`image`