Question

Given y'' - x^2y' + xy = 0 about (0,0)

a. Find two solutions of the given differential equation.
b. Solve the IVP if y(0) = 2, and y'(0) = 5

I am having trouble with the re-indexing and solving for ck's

Answer 1

By "ck" I'm assuming you're referring to the series solution's coefficients, i.e.
`y=\displaystyle\sum_(k\ge0)c_kx^k`.

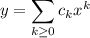
Differentiating gives


`y'=\displaystyle\sum_(k\ge1)kc_kx^(k-1)`

`y''=\displaystyle\sum_(k\ge2)k(k-1)c_kx^(k-2)`

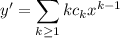
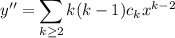
Substituting into the ODE yields


`\displaystyle\sum_(k\ge2)k(k-1)c_kx^(k-2)-x^2\sum_(k\ge1)kc_kx^(k-1)+x\sum_(k\ge0)c_kx^k=0`

`\displaystyle\sum_(k\ge2)k(k-1)c_kx^(k-2)-\sum_(k\ge1)kc_kx^(k+1)+\sum_(k\ge0)c_kx^(k+1)=0`

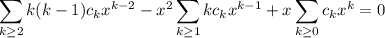
By extracting the first term (
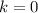
`k=0`) of the third series, you can consolidate the second and third series:


`\displaystyle\sum_(k\ge0)c_kx^(k+1)=\sum_(k\ge1)c_kx^(k+1)+c_0x`

Next, since the first series starts with a constant term while the other two start with a quadratic term, remove the first two terms:


`\displaystyle\sum_(k\ge2)k(k-1)c_kx^(k-2)=\sum_(k\ge4)k(k-1)c_kx^(k-2)+2c_2+6c_3x`

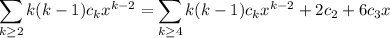
Now shift the index so that the series begins at the same starting index by replacing
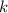
`k` with
`k+3`.


`\displaystyle\sum_(k\ge4)k(k-1)c_kx^(k-2)=\sum_(k\ge1)(k+3)(k+2)c_(k+3)x^(k+1)`

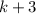
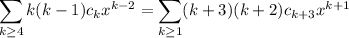
So now the series can be joined into one:


`\displaystyle\sum_(k\ge1)\bigg[(k+3)(k+2)c_(k+3)-kc_k+c_k\bigg]x^(k+1)`

which means the ODE is equivalent to


`\displaystyle\sum_(k\ge1)\bigg[(k+3)(k+2)c_(k+3)-(k-1)c_k\bigg]x^(k+1)+c_0x+2c_2+6c_3x=0`

It follows that
`2c_2=0\implies c_2=0` and
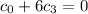
`c_0+6c_3=0`. Using this, you solve the recurrence


`(k+3)(k+2)c_(k+3)-(k-1)c_k=0\iff c_(k+3)=(k-1)/((k+3)(k+2))c_k`

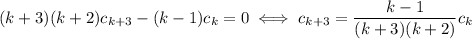
with the initial values
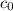
`c_0` and
`c_1`.

Because
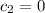
`c_2=0`, it follows that
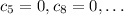
`c_5=0,c_8=0,\ldots`; in general,
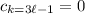
`c_(k=3\ell-1)=0` for all
`\ell\ge1`.

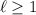
Also, because the RHS of the recurrence vanishes when
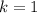
`k=1`, it follows that
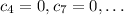
`c_4=0,c_7=0,\ldots`; or generally,
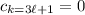
`c_(k=3\ell+1)=0` for
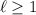
`\ell\ge1`, leaving you with only one not-necessarily-zero term of
`c_1`.

So the hard part is finding a solution for
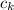
`c_k` when
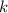
`k` is a multiple of 3. By finding the first few of these terms, you'll start to notice a pattern. Starting with
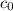
`c_0`, you find


`c_3=-\frac1{3*2}c_0`

`c_6=\frac2{6*5}c_3=-\frac1{6*5*3}c_0`

`c_9=\frac5{9*8}c_6=-\frac1{9*8*6*3}c_0`

`c_(12)=\frac9{12*11}c_9=-\frac1{12*11*9*6*3}c_0`

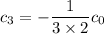
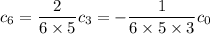
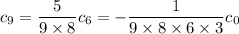
and so on, following a general pattern of


`c_(k=3\ell)=-(c_0)/((3\ell-1)\prod\limits_(i=1)^\ell 3i)`

`c_(k=3\ell)=-(c_0)/(3^\ell\ell!(3\ell-1))`

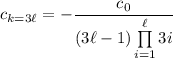
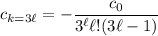
valid for
`\ell\ge1`.

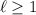
So the series solution is


`y=\displaystyle\sum_(k\ge0)c_kx^k`

`y=c_0+c_1x+c_2x^2+c_3x^3+c_4x^4+c_5x^5+c_6x^6+\cdots`

`y=c_0+c_1x+\displaystyle\sum_(\ell\ge1)c_(3\ell-1)x^(3\ell-1)+\sum_(\ell\ge1)c_(3\ell)x^(3\ell)+\sum_(\ell\ge1)c_(3k+1)x^(3k+1)`

`y=c_0+c_1x+\displaystyle\sum_(\ell\ge1)c_(3\ell)x^(3\ell)`

`y=c_0+c_1x-c_0\displaystyle\sum_(\ell\ge1)(x^(3\ell))/(3^\ell\ell!(3\ell-1))`

`y=c_0+c_1x+c_0\displaystyle\sum_(\ell\ge1)(x^(3\ell))/(3^\ell\ell!(1-3\ell))`

`y=c_1x+c_0\displaystyle\sum_(\ell\ge0)(x^(3\ell))/(3^\ell\ell!(1-3\ell))`

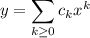
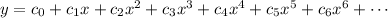
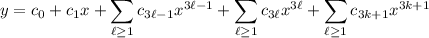
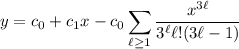
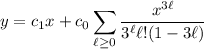
So the two solutions are
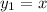
`y_1=x` and
`y_2=\displaystyle\sum_(\ell\ge0)(x^(3\ell))/(3^\ell\ell!(1-3\ell))`.

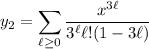
To solve the IVP, notice that when
`x=0`, you have


`y(0)=\displaystyle\sum_(k\ge0)c_kx^k=c_0=2`

`y'(0)=\displaystyle\sum_(k\ge1)kc_kx^(k-1)=c_1=5`

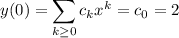
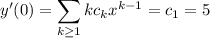
so the solution to the IVP is the same as that to the general solution with the unknowns replaced accordingly.