Let
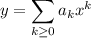
, so that
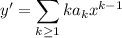
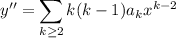
Substituting into the ODE gives
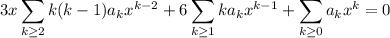

The first series starts with a linear term, while the other two start with a constant. Extract the first term from each of the latter two series:
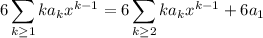
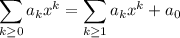
Finally, to get the series to start at the same index, shift the index of the first two series by replacing
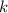
with
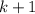
. Then the ODE becomes
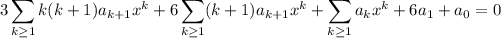
which can be consolidated to get
![\displaystyle\sum_(k\ge1)\bigg[(3k(k+1)+6(k+1))a_(k+1)+a_k\bigg]x^k+6a_1+a_0=0](https://img.qammunity.org/2018/formulas/mathematics/college/qzjex9y8e664kiaiq2tdenrtj61ddx0trq.png)
![\displaystyle\sum_(k\ge1)\bigg[3(k+1)(k+2)a_(k+1)+a_k\bigg]x^k+6a_1+a_0=0](https://img.qammunity.org/2018/formulas/mathematics/college/17683pf3es41pw9qb6ammc32i9y0udbgh3.png)
You're fixing the solution so that it contains the origin, which means

which in turn means
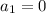
. With the given recurrence, it follows that
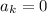
for all
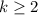
, so the solution would be
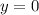
. This is to be expected, since

is clearly a singular point for the ODE.