Question

Find the sum of the first 9 terms of the sequence. Show all work for full credit.

2, -7, -16, -25, .

Answer 1

-7-2=-9, -16--7=-9 so there is a common difference, -9, so we know that this is an arithmetic sequence.

The sum of an arithmetic sequence is just the average of the first and last terms time the number of terms...

a(n)=a+d(n-1), in this case a(9)=2-9(8)=-70

So the sum is (2-70)(9/2)=-306

Answer 2

(-306)

Explanation:

We have to find the sum of the first 9 terms of the sequence

Sequence is 2, -7, -16, -25 ....

As we can see in this sequence there is a common difference of T₂ - T₁

= -7 -2 = (-9)

Formula to calculate the sum of n terms of an arithmetic sequence is
`s_(n)=(n)/(2)[2a+(n-1)d]`

Where a = first term = 2

d = common difference = (-9)

and n = number of terms = 9

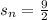`s_(n)=(9)/(2)` [ 2× 2 + (9-1) (-9) ]

=
`(9)/(2)` [4-72]

=
`(9)/(2)` [-68]

= 9 (-34)

= (-306)