Question

The total cost of producing a type of car is given by C(x) = 9000 - 20x + 0.02x^2, where x is the number of cars produced. How many carsshould be produced to incur minimum cost?

Answer 1

We can rewrite the equation in the standard form describing the total cost of production of a specific car as

`C(x)=0.02x^2-20x+9000`

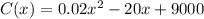
This is a quadratic equation. We want to solve how many cars will be produced for minimum cost. This means that we are looking at the part of the graph of the equation at a minimum. A quadratic equation can open upwards or downwards depending on the value of a. If a is positive, the parabola is opening upwards.

For the equation given, the value of a, which is 0.02, is positive. Hence, we can say that the graph of the equation is opening upwards and its vertex is at a minimum.

The value of x on vertex can be solved using the equation

`x=-(b)/(2a)`

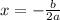
The value of b on the equation is -20. Substitute the values of a and b on the equation above to solve x, we get

`\begin{gathered} x=-((-20))/(2(0.02)) \\ x=500 \end{gathered}`

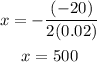
This x value represents the number of cars that can be produced at a minimum cost.

Answer: 500 cars