Question

Does the data in the table represent a direct variation or an inverse variation? Write an equation to model the data in the table.

x : 2 4 8 12
y : 10 5 5/2 5/3

A) direct variation ; y = 20/x
B) inverse variation ; xy = 20
C) direction variation ; y = 20x
D) inverse variation ; y/x = 20

Answer 1

B) xy=20

Inverse because it is of the form y=k/x, intuitively you can see that as x increases y decreases, hence "inverse variation".

Answer 2

Option B is correct

Inverse variation , xy = 20

Explanation:

Inverse variation states:

If
`y \propto (1)/(x)`

then the equation is in the form of:

`y = (k)/(x)`

or

xy = k ....[1]

As per the statement:

Given the data:

x : 2 4 8 12

y : 10 5 5/2 5/3

Let any value of x and y to find k:

x = 4 and y = 5

Substitute in [1] we have;

`4 \cdot 5 = k`

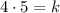
⇒20 = k

or

k = 20

then we get;

xy = 20

Check:

`xy = 20`

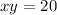
Substitute x = 12 and y = 5/3

`12 \cdot (5)/(3) = 20`

⇒
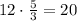
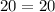`20 = 20` true.

Therefore, the the data in the table represent a inverse variation and an equation to model the data in the table is, xy = 20