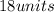Question

AD and MN are chords that intersect at point B.

What is the length of line segment MN?


I know the answer is 18 units but how did it get there I get 4 units

Answer 1

we know that

When two chords intersect each other inside a circle, the products of their segments are equal (Intersecting Chord Theorem)

so

In this problem

Step
`1`

Find the value of x

`AB*BD=MB*BN\\ 9*(x+1)=(x-1)*15\\ 9x+9=15x-15\\ 15x-9x=9+15\\ 6x=24\\ x=24/6\\ x=4`

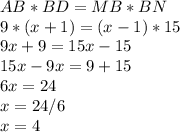
Step
`2`

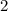
Find the value of MN

we know that

`MN=MB+BN\\ MN=(x-1)+15\\ MN=(4-1)+15\\ MN=3+15\\ MN=18`

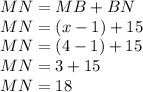
therefore

the answer is

the length of line segment MN is
`18 units`

Answer 2

When 2 chords intersect in a circle, the product of their segments are equal.

9 * (x +1) = 15 * (x -1)

9x +9 = 15x -15

24 = 6x

x = 4
SO,
Line AD = 9 + x + 1
Line AD = 14

Line MN = 15 + x -1
Line MN = 18