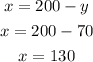Question

Theodore needs to mix a 20% saline solution with a 60% saline solution to create 200 milliliters of a 34% solution. how many millimeters of each solution must Theodore use?

Answer 1

130 ml of solution 1 and 70 ml of solution 2

Explanation

Step 1

Let

Volume of solution 1 ( 20% saline solution)=x

Volume of solution 2( 60 % saline solution)=y

Step 2

replace

Theodore needs to mix a 20% saline solution with a 60% saline solution to create 200 milliliters of a 34% solution

the volume of salt ( in solution 1)= 0.2 *volume of the solution 1

the volume of salt ( in solution 2)= 0.6 *volume of the solution 1

the volume of salt ( in mix)= 0.34 *volume of mix

replace,

`\begin{gathered} 0.2x+0.6y=0.34*200\text{ } \\ 0.2x+0.6y=68\text{ Equation(1)} \end{gathered}`

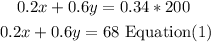
Also

volume os solution 1 + volume of solution 2 = volume of mix

replace,

`x+y=200\text{ Equation (2)}`

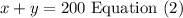
Step 3

use equatino (1) and (2) to find x and y

a) isolate x form equation (2)

`\begin{gathered} x+y=200 \\ x=200-y\text{ Equation (3)} \end{gathered}`

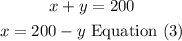
b) replace equation (3) in equation (1)

`\begin{gathered} 0.2(200-y)+0.6y=68 \\ 4-0.2y+0.6y=68 \\ 0.4y=68-40 \\ 0.4y=28 \\ y=(28)/(0.) \\ y=70 \end{gathered}`

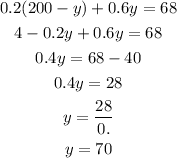
c) replace the valur of y =70in equation (3) to find x

`\begin{gathered} x=200-y \\ x=200-70 \\ x=130 \end{gathered}`