Question

Hikers spent the following amounts of time (in minutes) to complete a nature hike:48, 46, 52, 57, 58, 52, 61, 56.

a.find the mean and median times:
b.does one measure describe the data better than the other? Explain.
c. suppose another hiker takes 92 minutes to complete the hike. find the mean and median times including the new times.
d.does one measure describe the data better than the other now? Explain.

Answer 1

For A for the mean just add them all up which would be which is 430 and divide by the number of numbers there is so 430 divided by 8 = 53.75 and the median order them from least to greatest and find the one in the middle which is 52 and 56 when there's two just add them and then divide it by 2 which is 54

Hope this helped :)

Answer 2

Explanation:

Given that hikers spent the following amounts of time (in minutes) to complete a nature hike:48, 46, 52, 57, 58, 52, 61, 56.

Mean = sum/no of items =
`(430)/(8) =53.75`

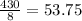
In ascending order this becomes

46, 48, 52, 52, 56, 57, 58, 61

Median is average of middle items

=
`(52+56)/(2) =54`

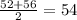
Here mean is less than median this implies there are more entries above the mean. i.e. skewed not symmetrical. For symmetrical distributions mean and median would be equal

c) If 92 is added to this data entry median becomes 56 but mean becomes

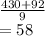`(430+92)/(9) \\=58` while median increases by 4.75

d) Median is better because it is not affected by outliers i.e. extreme values added to the set