Question

Dee wants to mix coffee worth $7 pound with coffee worth $4 a pound to get a mixture of 14 pounds $5 a pound . How many pounds of each must be mixed together to get the new blend?

Answer 1

`\bf \begin{array}{lccclll} &amount&price&cost\\ &-----&-----&-----\\ \textit{\$7/lb coffee}&x&7&7x\\ \textit{\$4/lb coffee}&y&4&4y\\ -----&-----&-----&-----\\ blend&14&5&14\cdot 5 \end{array}`

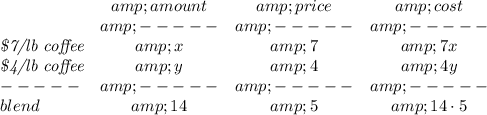
so.. whatever "x" and "y" amounts are, we know that, added together, they must yield 14lbs
thus x + y = 14

and whatever the cost of each is, 7x + 4y must be 14*5

7x+4y = 70
thus
`\bf \begin{cases} x+y=14\to \boxed{y}=14-x\\\\ 7x+4y=70\\ ----------\\ 7x+4\left( \boxed{14-x}\right)=70 \end{cases}`

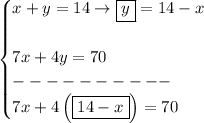
solve for "x", to see how much of the $7/lb type will be needed

what about the $4/lb one? well, y = 14 - x