Question

Calculus(Derivatives):

Show your work please!

Find the minimum and maximum points of f(x)=x^3+x^2-5x-2.

Answer 1

`f(x)=x^3+x^2-5x-2`

`\implies f'(x)=3x^2+2x-5=(3x+5)(x-1)`

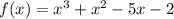
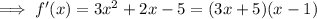
Critical points occur when
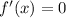
`f'(x)=0`, which happens for
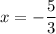
`x=-\frac53` and
`x=1`.

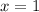
Check the sign of the second derivative at each critical point to determine the function's concavity at that point. If it's concave (
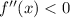
`f''(x)<0`), then a maximum occurs; if it's convex (
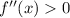
`f''(x)>0`), then a minimum occurs.

You have


`f''(x)=6x+2`

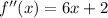
and so


`f''\left(-\frac53\right)=-8<0\implies f(x)\text{ is concave at }x=-\frac53`

`f''(1)=8>0\implies f(x)\text{ is convex at }x=1`

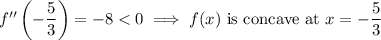
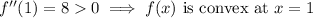
This means a maximum of
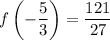
`f\left(-\frac53\right)=(121)/(27)` and a minimum of
`f(1)=-5`.