Question

Normal with a mean of 70 minutes and a standard deviation of 10 minutes. Using the 68-95-99.7 rule, what percentage of students will complete the exam in under an hour?

Answer 1

Note that
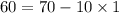
`60=70-10*1`, i.e. a student that completes the exam in one hour falls exactly one standard deviation (in the negative direction) from the mean.

Now, you're looking for the proportion of students that fall below this, i.e.
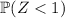
`\mathbb P(Z<1)`. The empirical rule states that approximately 68% of a normal distribution falls within one standard deviation of the mean. That is,


`\mathbb P(|Z|<1)=\mathbb P(-1<Z<1)=0.68`

This means that the proportion of students that fall outside this range is


`\mathbb P(|Z|>1)=\mathbb P(Z<-1)+\mathbb P(Z>1)=1-\mathbb P(|Z|<1)=0.32`

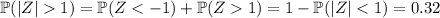
Because the distribution is symmetric, it follows that


`\mathbb P(Z<-1)=\mathbb P(Z>1)=\frac{0.32}2=0.16`

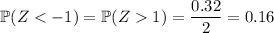
This means the percentage of students that complete the exam in under an hour is 16%.