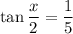is in quadrant I, so
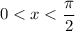
, which means
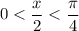
, so

belongs to the same quadrant.
Now,
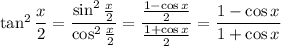
Since
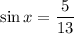
, it follows that
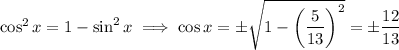
Since

belongs to the first quadrant, you take the positive root (
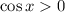
for

in quadrant I). Then
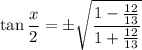
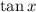
is also positive for

in quadrant I, so you take the positive root again. You're left with