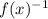Question

The demand function for an auto parts manufacturing company is given by f(x)= 100,000-2,500, where x represents price and f(x) represents quantity.

f^1 (x) = ________. In the inverse function, the variable x represents ________.
40-2500/x price
40+x/2500 quantity
40-x/2500
40+2500/x

Answer 1

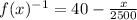`f(x)^(-1)=40-(x)/(2500)` Quantity

Explanation:

1) To find out the inverse function, let's geometrically do the test of the horizontal line by graphing this linear function.

f(x)=y

y=100,000-2500x.

Check the graph, the angular coefficient is -2500.

Suppose a horizontal line y=60. If y=60 touches the graph only once then this function is injective (one to one) and admits inverse function.

2) Let's algebraically do the procedures to find its inverse.

At first where is x, we change for y then we isolate y on the 1st member.

`y=100,000-2500x\\x=100,000-2500y\\2500y=100,000-x\\y=(100,000-x)/(2500)\\y=40-(x)/(2500)\\f(x)^(-1)=40-(x)/(2500)`

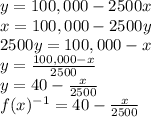
In this inverse function, the variable x represents quantity . Because the inverse function the Domain of its original function is the Range of it, as the Range of f(x) is the Domain of
`f(x)^(-1)`

Answer 2

Part 1) f(x)⁻¹ = 40 - x/2,500

Part 2) quantity

Explanation

f(x)= 100,000-2,500x

In finding the inverse of F(x) we make x the suject of the formula.

f(x)= 100,000-2,500x

2,500x = 100,000 - f(x)

x = 100,000/2,500 - f(x)/2500

x = 40 - f(x)/2,500

Now interchange x with f(x).

f(x)⁻¹ = 40 - x/2,500