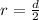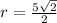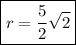Answer:
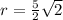
Explanation:
Triangles And Circles
If a right triangle is inscribed in a circle (or the circle is circumscribed around the right triangle), then the hypotenuse of the triangle is the diameter of the circle.
The right triangle has both legs of known lengths, thus the hypotenuse (the diameter of the circle is):
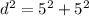

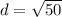
Since 50=2*25:
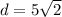
Thus the radius of the circle is: