Notation:
μ = mean
σ = standard deviation
Exam A:
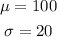
The score of the exam is 64, so we calculate the z-score given that scores on the exam are normally distributed. The formula of the z-score is:
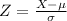
Now, for X = 64:
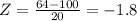
Exam B:
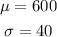
Now, we need to find a z-score equal to that of the score on Exam A. This z-score is -1.8, and the score on exam B should be:
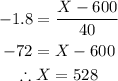
The score on exam B should be 528 in order to do equivalently well as he did on Exam A