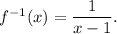Question

What is the inverse function of f(x) = x+1/x

Answer 1

`f^(-1) (x)= (1)/(x-1)`

Hope this helps!!

Answer 2

Answer: The required inverse function is given by

`f^(-1)(x)=(1)/(x-1).`

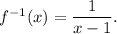
Step-by-step explanation: We are given to find the inverse function of the following function :

`f(x)=(x+1)/(x)~~~~~~~~~~~~~~~~~~~~~~~~~~(i)`

Let us consider that

f(x) = y, which gives that

`x=f^(-1)(y).`

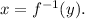
From equation (i), we have

`f(x)=(x+1)/(x)\\\\\\\Rightarrow y=(f^(-1)(y)+1)/(f^(-1)(y))\\\\\\\Rightarrow yf^(-1)(y)=f^(-1)(y)+1\\\\\Rightarrow yf^(-1)(y)-f^(-1)(y)=1\\\\\Rightarrow (y-1)f^(-1)(y)=1\\\\\Rightarrow f^(-1)(y)=(1)/(y-1).`

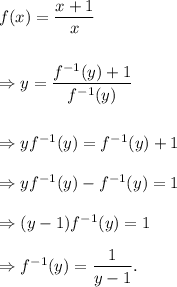
Thus, the required inverse function is given by

`f^(-1)(x)=(1)/(x-1).`